In one of my pen’n’paper groups we are playing “Niobaras Vermächtnis“. One of the riddles given in it involves solving a sudoku.
Its a variant of a regular sudoku called “greater than sudoku”, or in german “Vergleichssudoku”. Since I am to lazy to solve such a thing manually, I looked for a constraints solver to do that for me. I have never used something like that, so I started looking into different options:
- prolog -> I checked the wikipedia page and decided its to complicated for me^^
- clasp -> there was a python binding, I played around with that, but its python2 only
- z3 -> it has python3 bindings and a sudoku example. So lets use that.
I started from the example and added the greater-than constraints. They are encoded as strings, in horizontal and vertical direction.
Because the solver did not work, I added a hacky visualization to check the constraints visually. Then used some image processing to overlay that with the original riddle
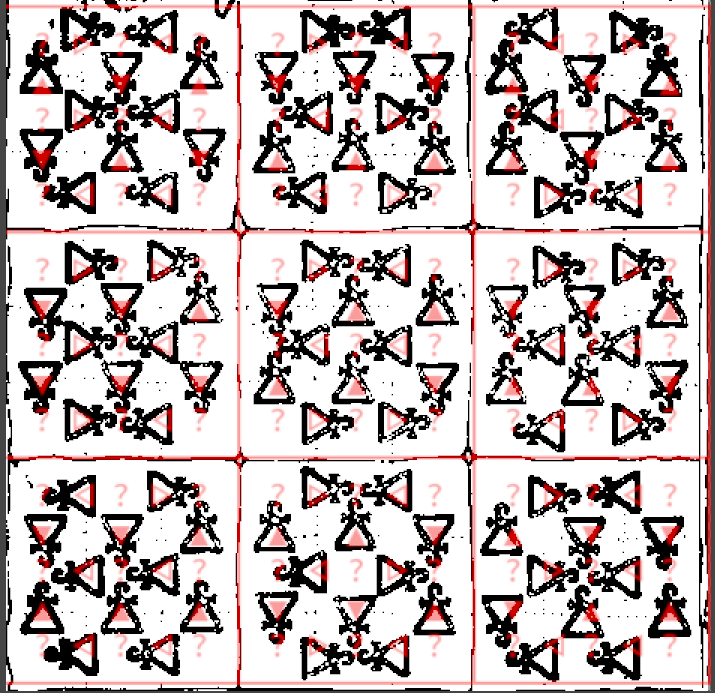
I did quite some more checking, and finally decided to test a known good sudoku. I found this one which solves fine
Thus, the reasonable explanation was that my solver is fine, but the riddle is not. Turns out, somebody already made the same discovery as me.
The people over at a DSA fanpage asboran.de already figured that out more than two years ago. After applying their proposed fix, the solver finally returns sat and produces an output:
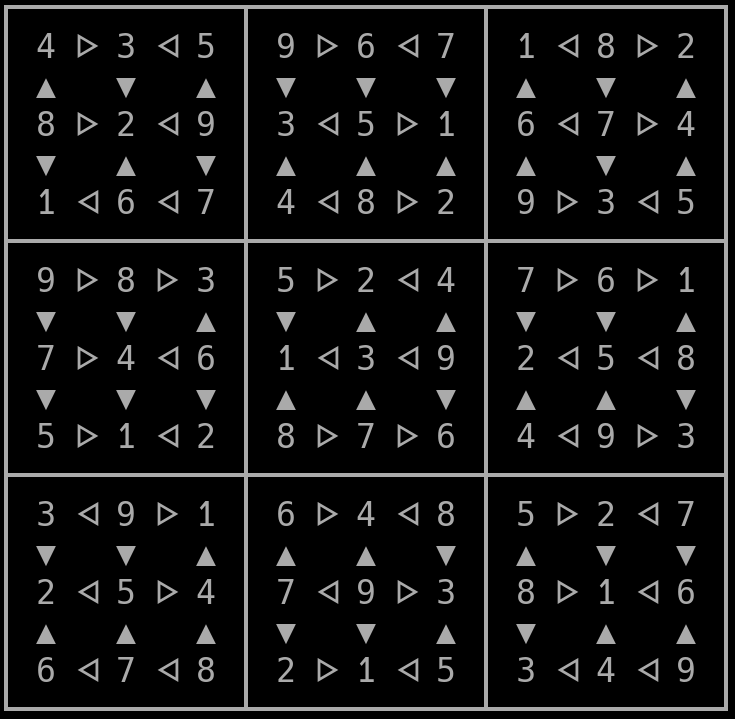
Here is my code if you like to laugh about it, or copy it. License is the same as the example I copied it from
from z3 import Int, Solver, And, Distinct, If, sat;
debug = False
# most of this code was taken and copied from the example at
# https://ericpony.github.io/z3py-tutorial/guide-examples.htm
# other reference for 'greater than sudokus'
# https://github.com/kit1980/grid-puzzle-solver/blob/master/greater-than-sudoku.ecl
# From niobaras vermächtnis (does not work)
# Horizontal constraints
GH = ["><><<>",
"><<><>",
"<<<>><",
">>><>>",
"><<<<<",
"><>><>",
"<>><><",
"<><>><",
"<<><<<"]
# vertical
GV = ["<>>>><",
"><>>><",
"<><><<",
"><><<>",
"><<<<>",
"><<>><",
"<<><<>",
"><><><", # original constraints with error
"<<<>><"]
# | this char was changed
GV[7] = ">>><><"
# from: https://plus.maths.org/content/puzzle-page-77
# we know a solution for this!
# Horizontal constraints
GH1 = ["><><<>",
"<<><<<",
"<<<<<>",
">>><<>",
"<>>><>",
">>>><<",
"<<<>><",
"><<<><",
"<>><><"]
# vertical
GV1 = ["<>><<<",
"<><><<",
"<>><<>",
"><<>><",
"><<>>>",
">>>>>>",
"><<><>",
"><><>>",
"<>><<<"]
# very hacky visualization
def print_matrix(m):
print("\n?????????????????????????????????????")
lineidx=0
for line in range(9):
print("?", end='')
colidx = 0
for col in range(9):
print(" {} ".format(str(m[line][col])), end='')
if (col+1) % 3 != 0:
ch = u"\u140a"
if GH[line][colidx] == ">":
ch = u"\u1405"
print(ch, end='')
colidx+=1
else:
print("?", end='')
if (line+1) % 3 == 0:
if (line != 8):
print("\n?????????????????????????????????????")
else:
a = ["i"]*9
for foo in range(9):
a[foo] = u"\u25bc"
if GV[foo][lineidx] == "<":
a[foo] = u"\u25b2"
print("\n? {} {} {} ? {} {} {} ? {} {} {} ?".format(a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8]))
lineidx+=1
print("\n?????????????????????????????????????")
## Begin adding constraints
###Jede Zahl nur eine Stelle; jede Spalte, jede Zeile, jedes Quadrat darin einmal jede Zahl.
# 9x9 matrix of integer variables
X = [ [ Int("x_%s_%s" % (i, j)) for j in range(9) ]
for i in range(9) ]
#Jede Zahl nur eine Stelle;
# each cell contains a value in {1, ..., 9}
cells_c = [ And(1 <= X[i][j], X[i][j] <= 9)
for i in range(9) for j in range(9) ]
cols_c = []
rows_c = []
for i in range(9):
# jede Zeile,
# each row contains a digit at most once
rows_c.append(Distinct([X[i][j] for j in range(9)]))
# jede Spalte,
# each column contains a digit at most once
cols_c.append(Distinct([X[j][i] for j in range(9)]))
#jedes Quadrat darin einmal jede Zahl.
# each 3x3 square contains a digit at most once
sq_c = [ Distinct([ X[3*i0 + i][3*j0 + j]
for i in range(3) for j in range(3) ])
for i0 in range(3) for j0 in range(3) ]
# the basic sudoku constraints
sudoku_c = cells_c + cols_c + rows_c + sq_c
# build our DSA horizontal constraints
xl= [0,1,3,4,6,7] # have a stupid lookup-thingy, only 6 out of 9 items have a constraint
h_c = []
for lidx, line in enumerate(GH, start=0):
for cidx, c in enumerate(line, start=0):
if c == ">":
h_c.append(X[lidx][xl[cidx]] > X[lidx][xl[cidx]+1])
#print("X{}_{} > X{}_{}".format(lidx, xl[cidx], lidx, xl[cidx]+1))
else:
h_c.append(X[lidx][xl[cidx]] < X[lidx][xl[cidx]+1])
#print("X{}_{} < X{}_{}".format(lidx, xl[cidx], lidx, xl[cidx]+1))
# build our DSA vertical constraints
v_c = []
for ridx, row in enumerate(GV, start=0):
for cidx, c in enumerate(row, start=0):
if c == ">":
v_c.append(X[xl[cidx]][ridx] > X[xl[cidx]+1][ridx])
#print("X{}_{} > X{}_{}".format(xl[cidx], ridx, xl[cidx]+1, ridx))
else:
v_c.append(X[xl[cidx]][ridx] < X[xl[cidx]+1][ridx])
#print("X{}_{} < X{}_{}".format(xl[cidx], ridx, xl[cidx]+1, ridx))
if debug:
print("Cells 1..9:", cells_c)
print("Rows:", rows_c)
print("Cols:", cols_c)
print("SubSquares:", sq_c)
print("Horizontal:", h_c)
print("Vertical:", v_c)
for co in sudoku_c + h_c + v_c:
print (co)
# print a empty matrix so we van visually inspect the constraints
empty = [["?"]*9]*9
print_matrix(empty)
# create a solver, add all constraints
s = Solver()
s.add(sudoku_c + h_c + v_c)
if s.check() == sat:
print("done")
m = s.model()
r = [ [ m.evaluate(X[i][j]) for j in range(9) ]
for i in range(9) ]
print_matrix(r)
else:
print ("failed to solve")
print (s.statistics())
